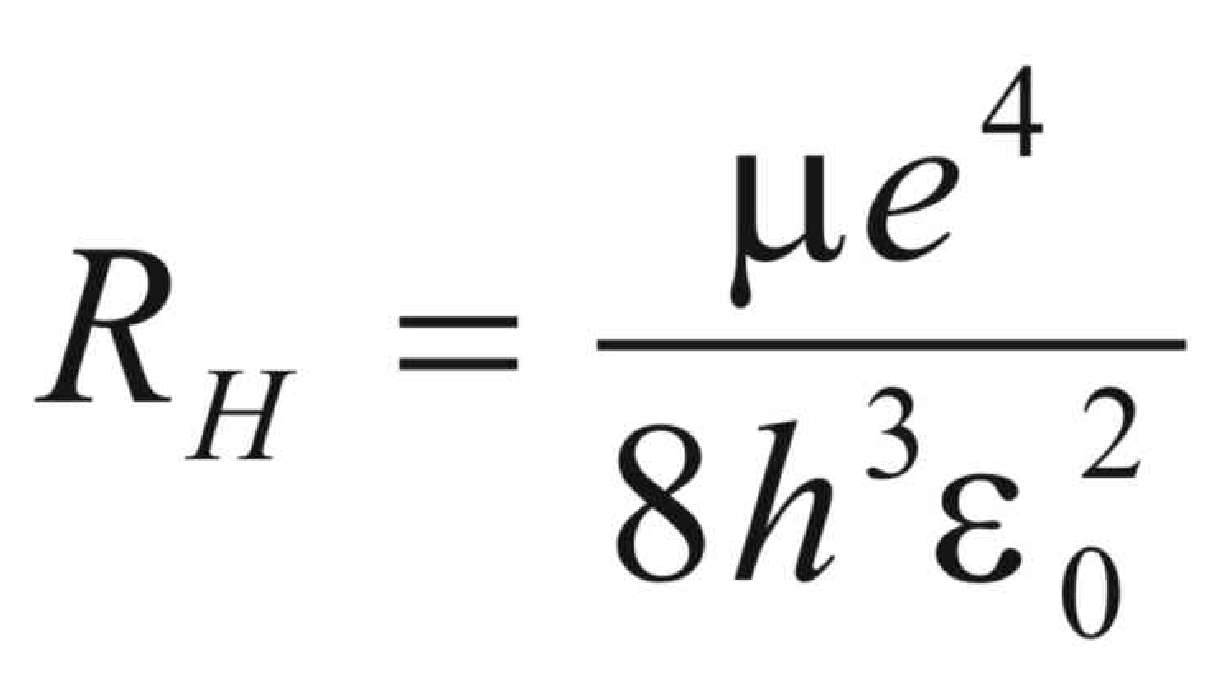Estimated read time: 5-6 minutes
This archived news story is available only for your personal, non-commercial use. Information in the story may be outdated or superseded by additional information. Reading or replaying the story in its archived form does not constitute a republication of the story.
In the spirit of the inevitable end-of-the-year lists of the top 5 of everything, here's a list of the top five most interesting numbers of all time - and not just for 2011. These numbers are important to our everyday lives whether we know it or not.
Coming in fifth is the Rydberg Constant, R∞, which is about 1.097x10^7 per meter. Units matter - units always matter. This Rydberg Constant is simple enough in concept but rather large in complexity.
You might not think this is all that interesting, but the folks over at CSI: Miami sure do. Here's why: All atoms absorb energy and give off energy — different kinds of energy from light to heat to cosmic gamma rays. Sometimes atoms absorb enough energy from the heat around them that they begin to vibrate. The vibration in turn causes the atoms to give off infrared light different than what they absorbed. The Rydberg constant helps us understand the unique spacings between the colors of light emitted by atoms.
You might not think this is all that interesting, but the folks over at CSI: Miami sure do.
This fact is often utilized in analyzing different gases. Have you ever heard someone on a TV crime show say something like, "I'm gonna send that sample over to 'trace'." That means they are sending it to be analyzed for traces of stuff on or in the sample. Whichever method they use, the Rydberg constant helps scientists catalog unique signatures from each element. The catalogs are then used by police labs to catch the criminals.
Number four is h, which is also known as Plank's constant. It has a value of roughly 6.626x10^-34 Joule seconds. The units are important here as they add context and meaning to the number.
Plank's constant is the number used to numerically convert the frequency of light (color) into energy. For example, the energy from a light bulb can be calculated thanks to Plank's constant. More importantly, knowing the energy of light allows us to calculate how much of that light can be converted into electrical energy via the photon-electric effect by a solar-panel.
Next is Boltzman's constant, k, coming in at number three. Boltzman's constant is another conversion, similar to Plank's constant, and was essential for night vision goggles to become a reality. Its value is about 1.38x10^-23 Joules per Kelvin. Have you ever seen the burner on a stove glow red and want to know why? It is because the burner is hot and emits visible light. If you measure the color of the light coming from a warm object, Boltman's constant will let you figure out the exact temperature.
Yes, infinity is a number, and as you might expect it can be rather difficult to pin down an exact numerical value for it.
The reverse is true, too. If you know how hot something is, you will be able to predict how much light and the color of the light that will be emitted. Based on the color of a distant star and other factors, scientists can determine the star's temperature.
Number two is infinity, or ∞. Yes, infinity is a number, and as you might expect it can be rather difficult to pin down an exact numerical value for it. As a matter of fact there are several "sizes" of infinities, some infinately bigger than other infinities. Two sizes are countable infinities and uncountable infinities.
Take the counting numbers, 1, 2, 3, 4, etc, as an example. You can count them in an orderly, sequential fashion. Even though you can not count the exact number, they are ordered and can be counted in that order infinitely.
Any infinity is countable if it corresponds to the normal counting numbers (or positive integers) on a one-to-one bases. All rational numbers, your ordinary fractions, are part of a countable infinity, just like the positive integers. Infinities that are not countable are more tough to define, but one example is the real numbers - that's all the rational numbers, plus all the irrational numbers like pi, tau, the golden ration, and infinitely infinite more.
Topping this list at number one is e. Numerically it is roughly 2.718 and, unlike most of the others in this list, it is unitless. It is the base for the natural logarithm. Does that ring a bell? Probably not. Well, let's put it differently. There are two reasons e is makes the number one spot.
First, it beautifully ties together other numerical entities in math in what is called Euler's Identity. Combined with the imaginary number, i, and with π, which you might recognize, it unfolds trigonometric into functions like sine and cosine.
This unfolding allows engineers and mathematicians to turn complex equations into simple addition and subtraction. Equations used to describe communication between land line phones are an example. Communication between antennas, like the ones in your cell-phone and on the tower is another example of what engineers have been able to build using equations simplified using e in Euler's Identity.
The second reason e is on this list is because of Professor Moon. Years ago at Utah State Univiversity, he drilled the importance of e and Euler's Identity into the mushy heads of the engineering students. He called it identity the "deathbed identity," meaning that every electrical engineer should know this identity so well that they will quote it to their family and friends as they lay dying. e is that important.
So whether you know it or not, you already use these numbers just by watching TV crime, using a phone, counting or just being warmer than absolute 0.